Neurônios Artificiais – Função de Ativação no modelo Perceptron


O resultado dessa combinação indicará se o neurônio artificial fará ou não disparo do sinal de programação.
Introdução
Antes de falar da função de ativação, vamos relembrar um pouco sobre o modelo perceptron. Recomendamos a leitura do primeiro artigo da série sobre neurônio artificial.
No modelo perceptron, temos sinais de entrada que estão associados aos pesos. Em seguida, conforme discorre o artigo que citamos, a função de decisão – que indica se o neurônio artificial vai ou não disparar o sinal – faz uma combinação linear com os valores de entrada. Relembrando:
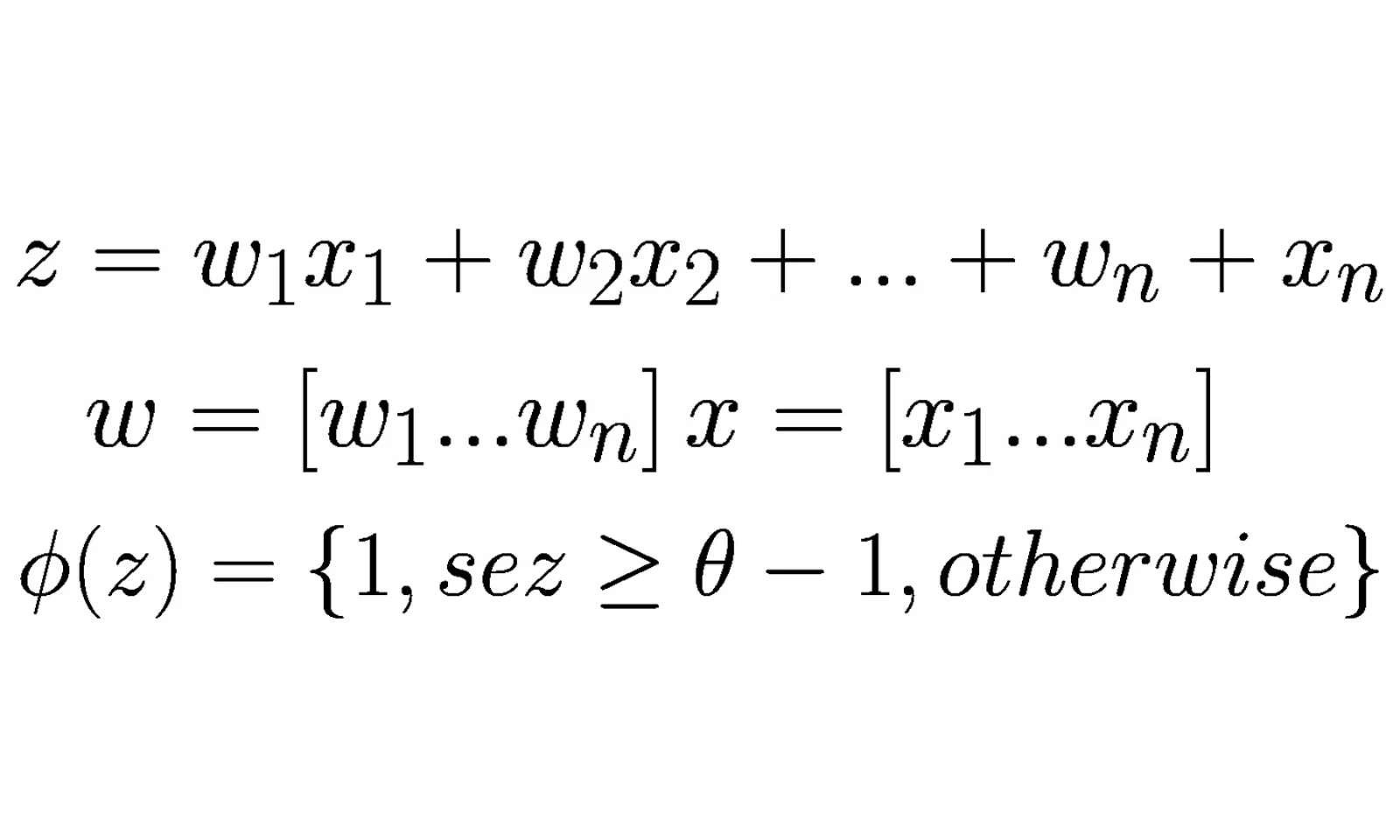
A Função de Ativação
A função de ativação é usada para determinar o valor de saída da combinação linear que estudamos. Aplicamos a função de ativação no resultado dessa combinação linear ou na função de decisão. No final, a ativação converte o resultado em 1 ou -1. Vale ressaltar que existem alguns tipos diferentes relacionados à função de ativação: sigmoid, tanh, entre outros.
A escolha da função de ativação depende de cada caso. É necessário entender o problema e modelar a rede com a melhor função para o problema que estamos tentando resolver. Por isso, é necessário entender as técnicas que ajudam a escolher a melhor função de ativação, mas esse é um assunto para outro artigo… Neste, vamos tentar primeiro entender como a função de ativação funciona e como ela se encaixa no modelo perceptron.
No artigo que citamos anteriormente, usamos a seguinte imagem para ilustrar, vamos rever:
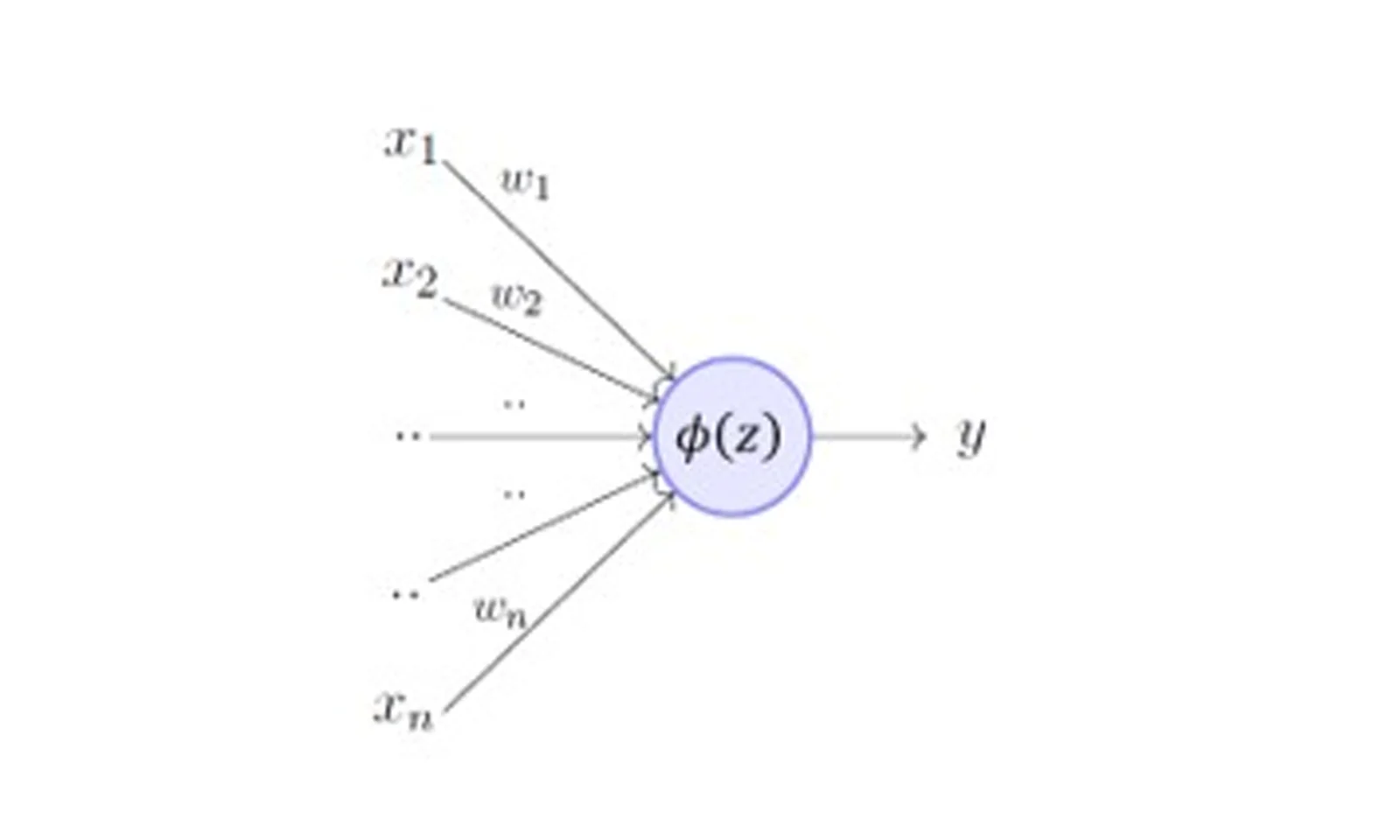
Vamos dizer que a nossa função de ativação será, f(x). Uma vez que temos a função, vamos encaixar no modelo perceptron, junto a combinação linear ou função de decisão, como foi dito. Veja: f(ϕ(z)). Com base na ilustração utilizada acima, vemos uma nova ilustração, agora com a função de ativação:
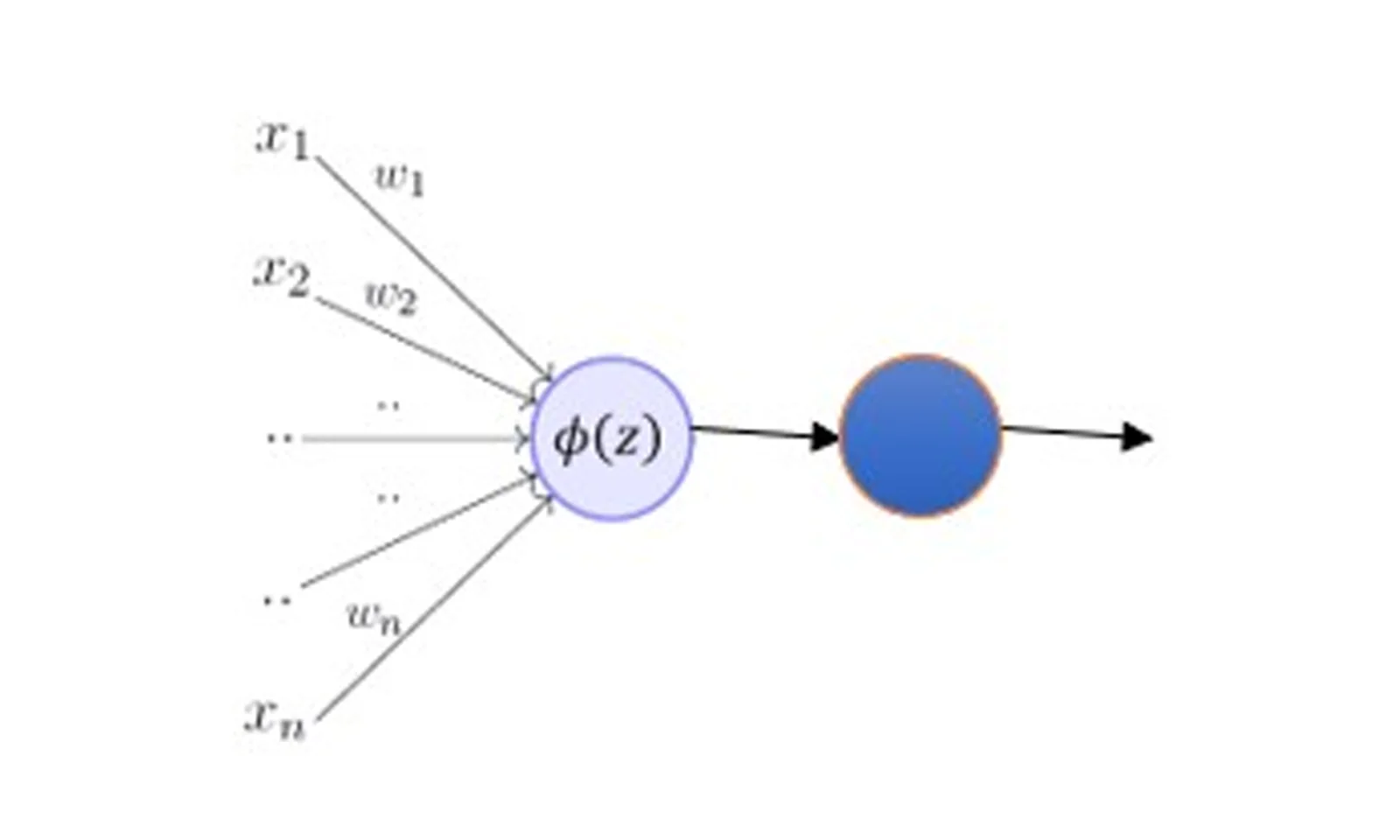
Conforme mencionado, existem algumas opções de funções de ativação. Para o nosso exemplo ilustrativo, vamos escolher a função sigmoid. Em linhas gerais, essa função converte o valor em um espaço binário, o que se torna útil em termos estatísticos. Podemos, então, transformar nosso resultado em um número entre -1 e 1, o que facilita a interpretação.
Uma definição formal da função sigmoid seria:
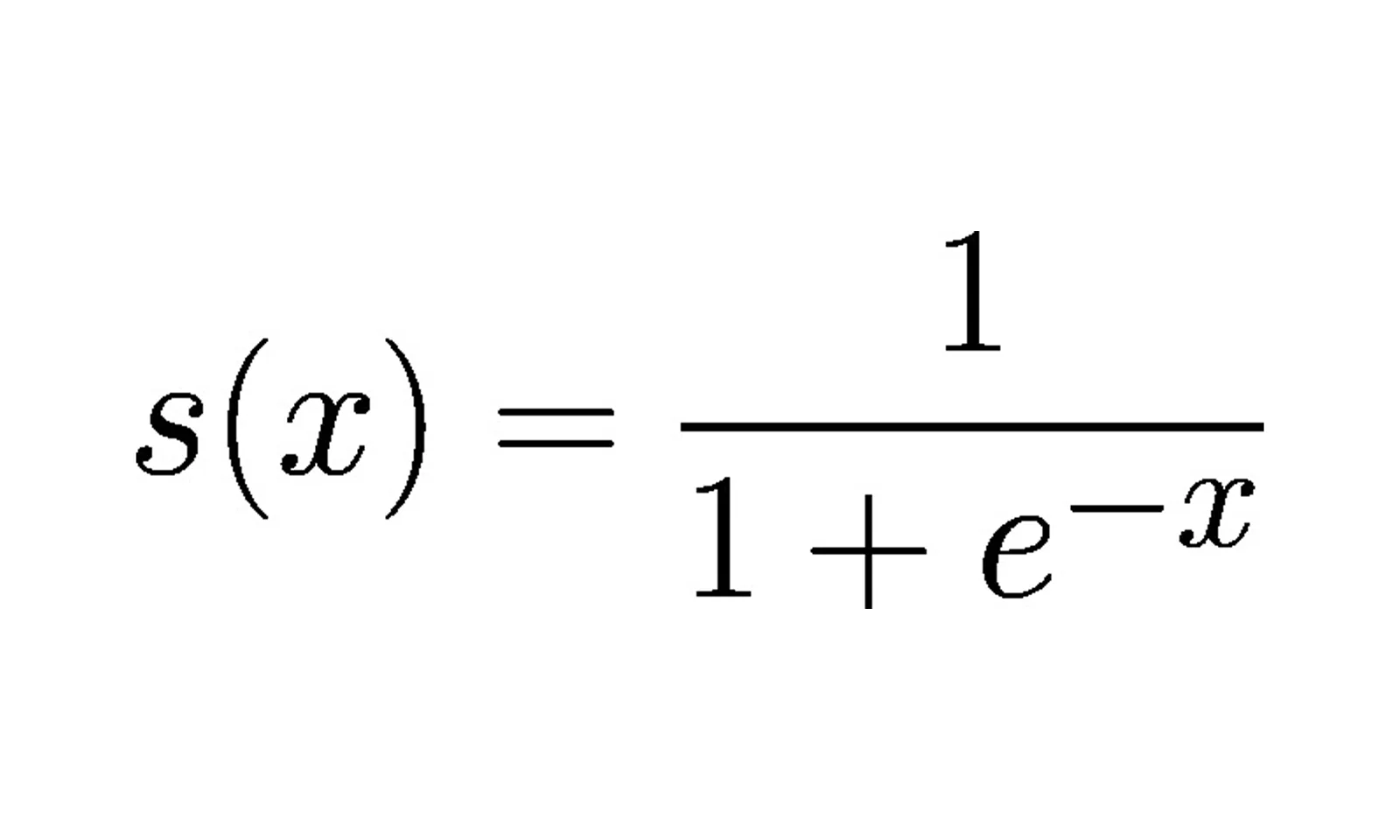
Considerando o exemplo da figura acima:
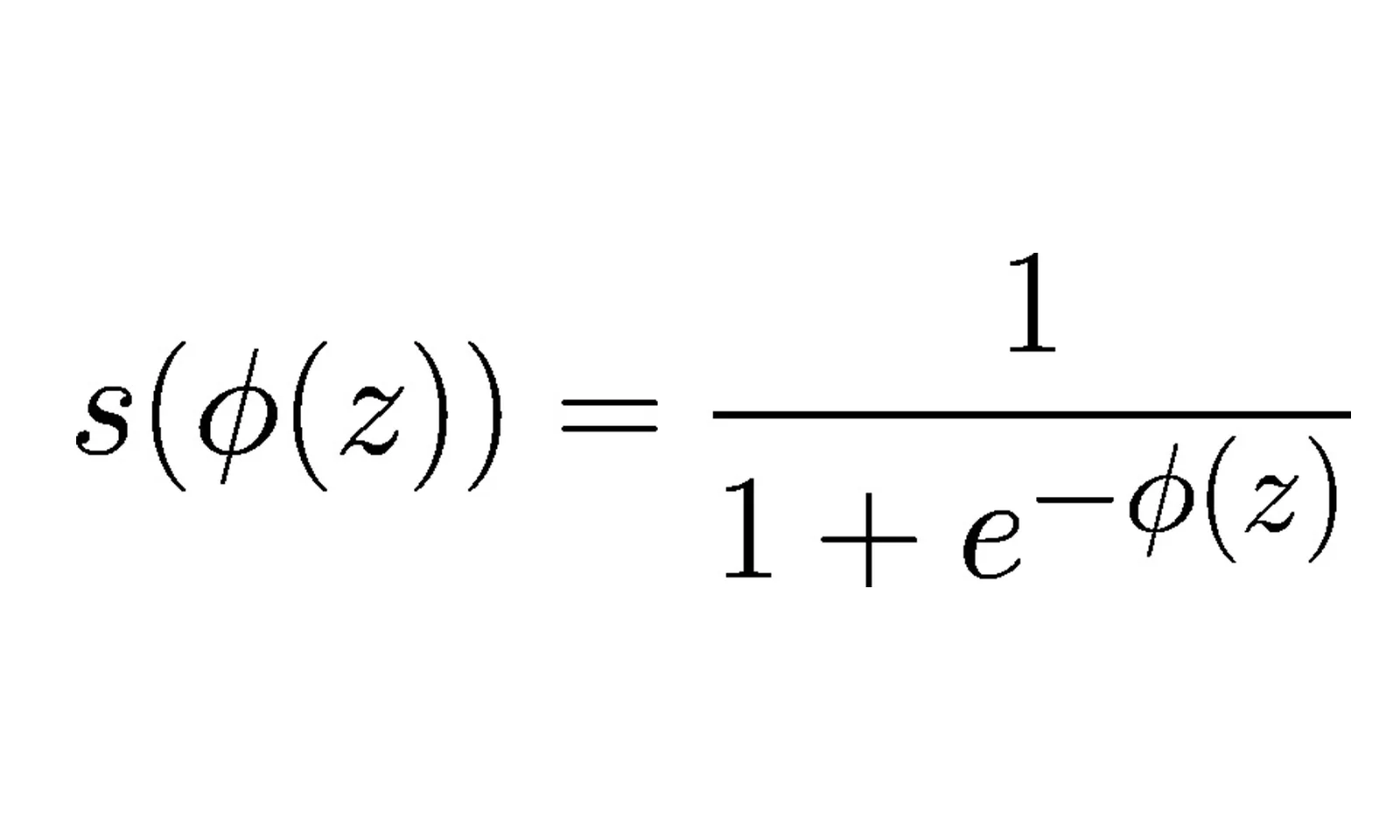
Lembrando do artigo em que fizemos a implementação do modelo perceptron, com um exemplo extremamente simples e considerando um dataset bem pequeno sobre times, vamos rever o resultado:

Voltando à nossa função de ativação, podemos ver no quadro acima dois resultados: vamos escolher o resultado do time A, temos, ϕ(z)=0.5, agora, olhando novamente a função de ativação:
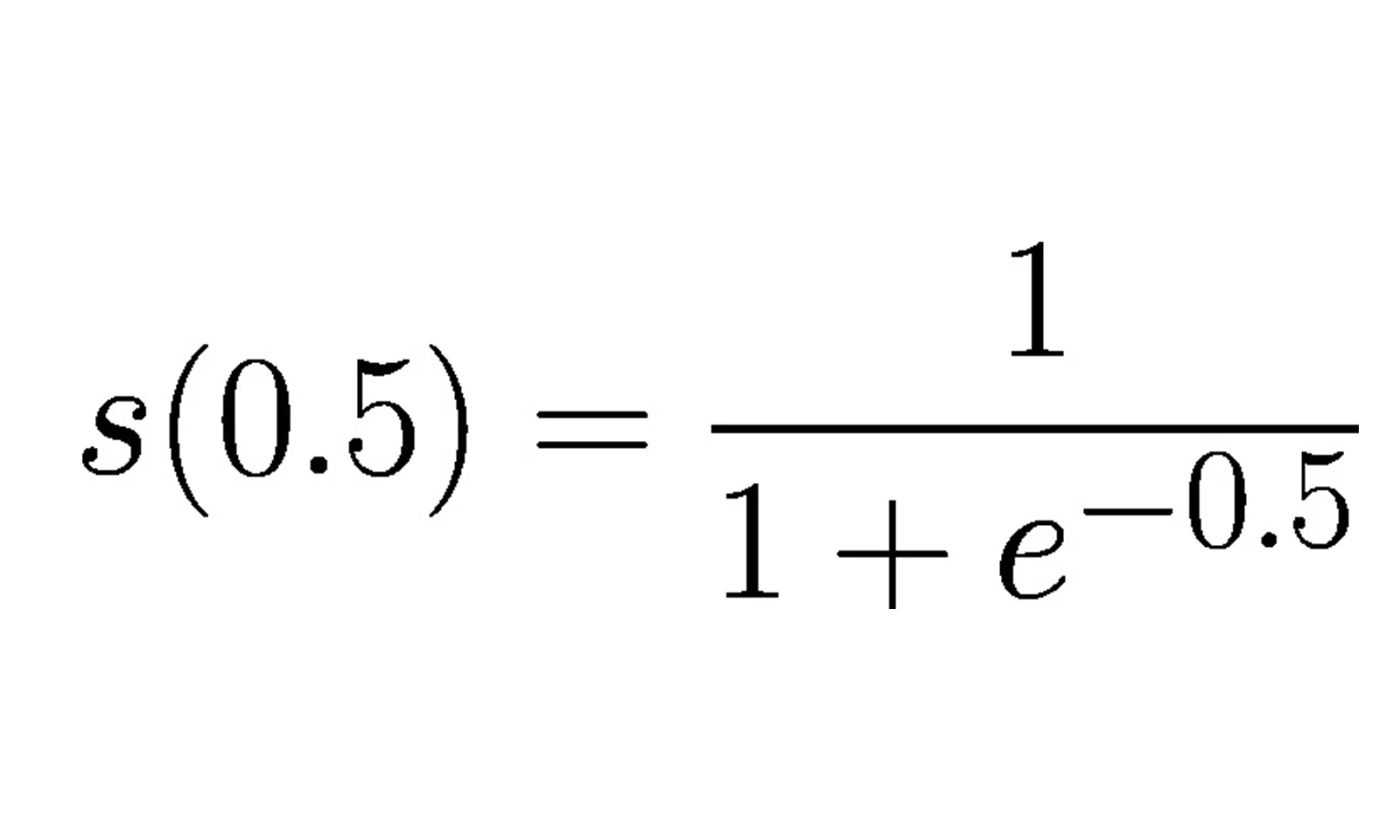
A variável e , é o número de Euller. Como não é escopo deste artigo tratar da origem dessa variável, vamos tentar associar o funcionamento da função de ativação com as possibilidades de interpretação de seus resultados. Aqui, nosso interesse epistemológico, se traduz em entender se o resultado, pertence ou não a determinada classe, no tocante a nossa intenção de classificação de determinado dataset.
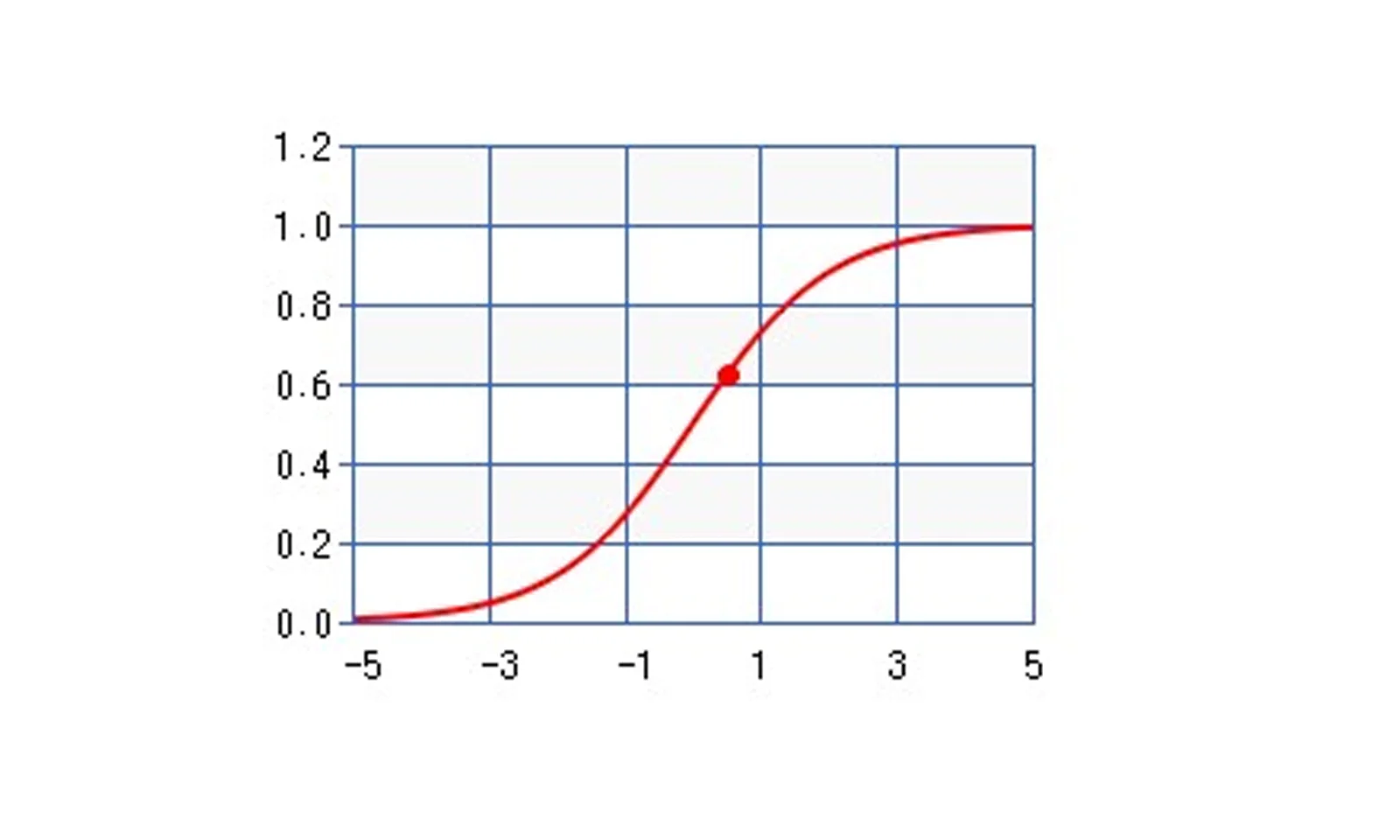
O resultado da sigmoid do nosso exemplo, é: 0.8175. Abaixo um exemplo de como calcular a sigmoid em Python:

Vejamos a sigmoid para o nosso exemplo:
Conclusão
Podemos perceber que a função de ativação é executada com resultado da combinação linear, que antes, foi executada pela função de decisão. Tratamos nesse artigo da função de ativação sigmoid, apenas para ilustrar o que é a função de ativação. Existem outras funções disponíveis, por isso, quando o usuário estiver construindo sua neural artificial, deverá procurar entender qual função de ativação é a escolha mais próxima de sua necessidade.
Sabemos agora que a cada época esse processo se repetirá, por quantas épocas a rede foi programada para ser treinada. Veremos mais à frente, que existem ainda técnicas para redução de erros e alguns conceitos que são importantes enquanto estamos buscando um bom modelo.
Referências
https://keisan.casio.com/exec/system/15157249643325
https://deepai.org/machine-learning-glossary-and-terms/sigmoid-function
https://www.youtube.com/watch?v=LW9VnXVIQt4
https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
https://medium.com/mlearning-ai/a-little-about-perceptrons-and-activation-functions-aed19d672656
https://www.simplilearn.com/tutorials/deep-learning-tutorial/perceptron





